DeepRank,一个基于列表排序的推荐算法
学术主页:英文主页
论文下载:DeepRank: Learning to Rank with Neural Networks for Recommendation
欢迎大家引用,谢谢!
代码下载:tensorflow code
目前只有当初写的 tensorflow 版本,pytorch 版本等有空会补充。
前言
当前,大部分推荐算法都是基于用户-商品的交互信息来预测两者之间将会产生的评分值或者是可能性。最近几年,深度学习在推荐算法中研究越来越多,但是大部分算法是 point-wise 的,还有不少 pair-wise 的,没有 list-wise 的。基于这个情况下,我们提出了一个基于 list-wise 排序的深度学习推荐算法,简称 DeepRank,即基于深度学习的排序推荐模型。
相关内容
基于列表排序的算法中,只有 2010 年的 ListRank-MF 算法,一个传统的矩阵分解模型。现在假设用户 \(u\),他有一个商品列表 $l_u$,计算他曾经评价过的一个商品 $i$,是排在他列表中最高位置的可能性:
\(P_{l_{u}}(r_{ui})=\frac{g(r_{ui})}{\sum_{k=1}^K g(r_{uk})} \tag{1}\)其中,$r_{ui}$ 是用户 $u$ 对商品 $i$ 的评分,$K$ 是用户推荐列表 $l_u$ 中商品的个数,即 $l_u$ 的长度, $g(\cdot)$ 是一个单调递增的函数。
然后,采用交叉熵来衡量损失:
\(\mathcal L(p,q)=\sum_{i=1}^K P_{l_u} \left(r_{ui}\right)logP_{l_u}\left(f \left(p_u^Tq_i \right) \right) + \frac{\lambda}{2}(\| p \|_F^2 + \| q \|_F^2)\tag{2}\)其中, $N$ 和 $M$ 分别是用户和商品的数目, $\lambda$ 是正则项系数, $p$ 和 $q$ 分别表示用户和商品的特征向量矩阵, $p_u$ 和 $q_i$ 分别表示用户 $u$ 和商品 $i$ 的特征向量, $f(\cdot)$ 是 Logistic 函数, 为了限制 $p_u^Tq_i$ 的取值范围。
但是,该模型存在两个问题:传统的 MF 模型缺少对数据非线性和深度特征的学习;只计算第一个商品的概率,而不是前 k 个商品的概率。
DeepRank
为了解决 ListRank-MF 算法存在的问题,我们提出了 DeepRank。采用深度学习模型来建模,来预测未来前 k 个商品的排序情况。现给定一个评分矩阵 \(R\),其中有 $N$ 个用户和 $M$ 个商品,我们重新定义可能性矩阵:
\(y_{ui}=\left\{\begin{matrix}1, \quad 如果\ r_{ui}>0\\
0,\quad\quad 其他 \quad \
\end{matrix}\right.\)
框架

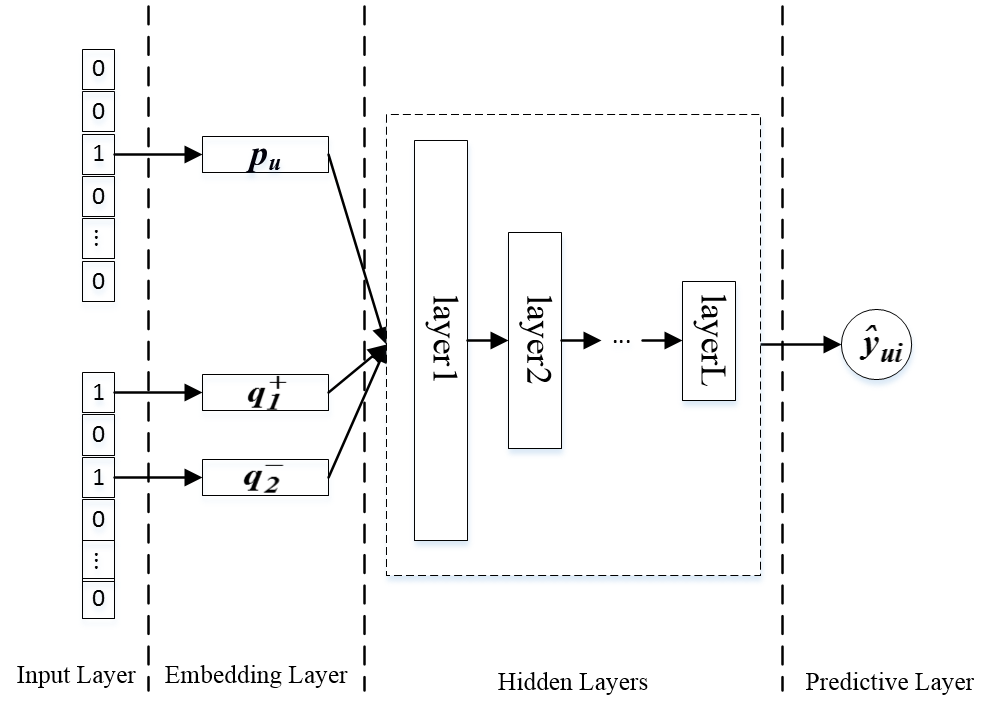
图一:基于列表排序的 DeepRank 框架
如图一所示,DeepRank 总共四层:输入层、嵌入层、隐含层和预测层。输入用户 $u$ 和他的 $K$ 个商品,输出 \(\hat{y}_{ui}\),最后用 $softmax$ 函数来预测这些商品的概率:
\(\hat{y}_{ui}=softmax(x_{ui})\)其中 $x_{ui}$ 是隐含层的输出,即:
\(\hat{y}_{ui}=\frac{e^{x_{ui}}}{\sum_{k=1}^K e^{x_{uk}}}\)因为我们是对前 $k$ 商品进行预测,计算它们的概率分布:
\(P_{l_{u}}\left( S(i_1,i_2,\cdots,i_K) \right)=\prod_{j \in l_u^+}\hat{y}_{uj}\prod_{k \in l_u^-}(1-\hat{y}_{uk})\)其中 $S(i_1,i_2,\cdots,i_K)$ 表示列表 $l_u$ 中商品, $l_u^+$ 和 $l_u^-$ 分别表示其中的正样本和负样本。
然后,采用交叉熵来计算损失函数:
\(f(y,\hat{y})=-\sum_{u=1}^N \left( \sum_{i \in l_u^+} log\hat{y}_{ui}+ \sum_{j \in l_u^-}log(1-\hat{y}_{uj})
\right)
\tag{3}\)
其中 \(y_{ui}\) 和 \(\hat{y}_{ui}\) 分别表示预测值和真实值。
其中的正则项如下:
\(\Omega(\Theta)=\sum_{l=1}^L \| \mathbf{w}_l \|_F^2 + \sum_{u=1}^N \| \mathbf{p}_u \|_F^2 + \sum_{i=1}^M \| \mathbf{q}_i \|_F^2\)
Pair-wise DeepRank
这其实是 list-wise 的一个简化版本。列表排序其实是很费时的,时间成本太大。为了提高效率,将原模型进行一定程度的简化,就是 pair-wise 模型。示意图如下所示:
图二:配对排序的 DeepRank 框架
它的损失函数:
\(f(y,\hat{y})=-\sum_{u=1}^N \left( \sum_{i \in I_u^+} log\hat{y}_{ui}+ \sum_{j \in I_u^-}log(1-\hat{y}_{uj})
\right)
\tag{4}\)
与其他经典算法的关系
与 ListRank-MF 的关系
在公式 (1) 中, ListRank-MF 模型的 $g(x)=e^x$ ,所以 $P_{lu}(r{ui})$ 可以看成是 softmax 函数。为了与我们的模型一致, 我们定义 \(y_{ui}'=P_{l_{u}}(r_{ui})\),且 \(\hat{y}_{ui}'=P_{l_{u}}\left( f \left(p_u^Tq_i \right) \right)\),那么公式 (2) 重写成:
\(\mathcal L=-\sum_{u=1}^N\sum_{i\in I_u^+} y_{ui}'log\hat{y}_{ui}'+ \lambda \Omega(\Theta)\tag{5}\)
根据公式 (5),我们发现不同之处:ListRank-MF 只对正样本进行建模。而我们采用BPR中的模型,同时考虑了正、负样本。如果,我们只考虑正样本, 那么 ListRank-MF 就可以看是 没有隐含层和 sigmoid 函数的 top-one list-wise DeepRank 模型。
相比较 ListRank-MF,该模型有三个有时候:
1) DeepRank 对 top-n 进行建模, 而非 ListRank-MF 采用的 top-one, 建模信息更充分,覆盖面更广;
2) DeepRank 用神经网络来学习非线性特征,表达能力更强;
3) DeepRank 因为独特的结构,可以设置用户和商品不同的特征向量维度,而 ListRank-MF 等模型因为要进行內积计算,它的用户和商品特征数目是一样的。我们这样更灵活,鲁棒性更强。
与 BPR 的关系
BPR 是最经典的配对算法。它的核心思想是用户认为已经购买的商品肯定比那些尚未购买的商品好。它的损失函数定义:
\(\mathcal L=\sum_{u=1}^N\sum_{i\in I_u^+ ,j \in I_u^-}- log\hat{x}_{uij}+ \lambda \Omega(\Theta)\tag{6}\) \(\hat{x}_{uij} =p_u^Tq_i - p_u^Tq_j\)
其中 \(\sigma(x)=1/(1+exp(-x))\) 是 sigmoid 函数。
在公式 6 中,我们定义 \(\hat{y}_{uij}=\sigma(\hat{x}_{uij})=1/(1+exp(-\hat{x}_{uij}))\) 后:
\(\mathcal L=\sum_{u=1}^N\sum_{i\in I_u^+ ,j \in I_u^-}- log\hat{y}_{uij}+ \lambda \Omega(\Theta)=-\sum_{u=1}^N \left( \sum_{i \in I_u^+} log\hat{y}_{ui}
+ \sum_{j \in I_u^-}log(1-\hat{y}_{uj})
\right)+ \lambda \Omega(\Theta)
\tag{7}\)
然后我们发现公式 (7) 和公式 (4) 是一样的。
在 DeepRank 中, \(\hat{x}_{uij}=f_{MLP}(\mathbf{p}_u,\mathbf{q}_i)\), 且
\(\hat{y}_{uij}=softmax(\hat{x}_{uij})=\frac{e^{x_{ui}}}{e^{x_{ui}}+e^{x_{uj}}}=\frac{1}{1+e^{-(x_{ui}-x_{uj})}}=\frac{1}{1+e^{-x_{uij}}}\)
BPR中, $p_u$ 和 $q_i$ 之间的交互函数是內积相乘的。现在假设我们的模型没有隐含层,我们可以得到 \(\hat{x}_{uij}=p_u^Tq_i\), 且 \(\hat{y}_{uij}\) 是 sigmoid 函数, 和 BPR 中定义的一样。 因此,我们可以将 BPR 看成是 pair-wise DeepRank 的简化模型。而 pair-wise DeepRank 又是 DeepRank 的简化模型。
实验
我们用了三个数据集:MovieLens100K,MovieLens1M 和 Yahoo! Movie。评估指标是 $NDCG$ 和 $HR$,实验结果如下所示:
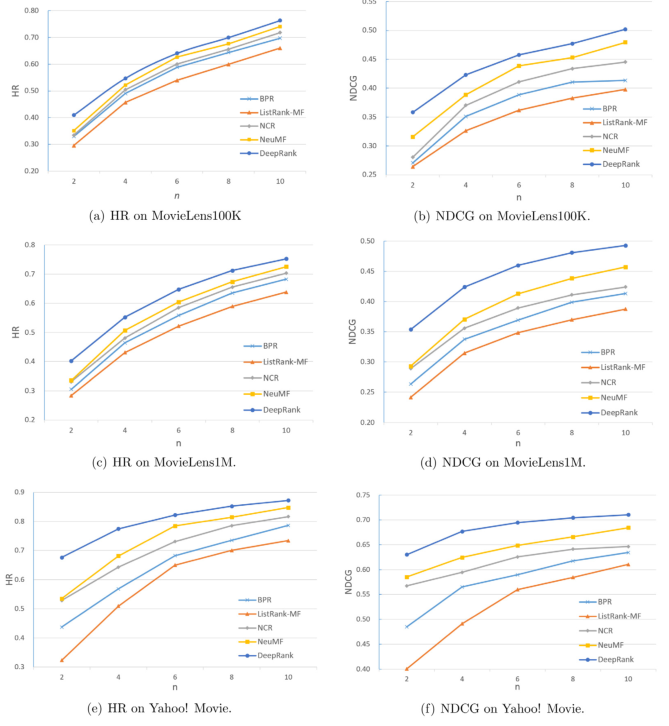
接下来我们看一下列表中正样本个数对实验结果的影响:
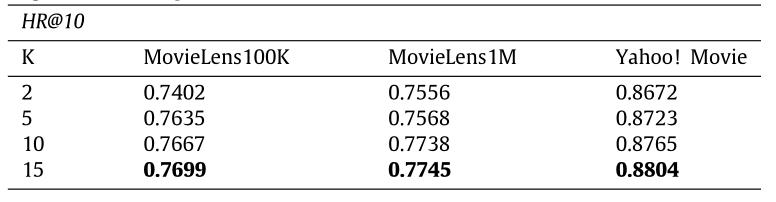
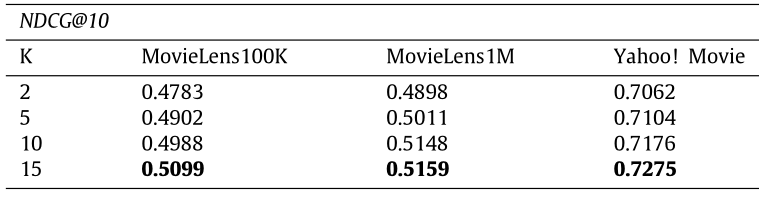
表三、表四:列表中正样本数目 K 的影响
然后,我们查看一下模型的耗时情况:
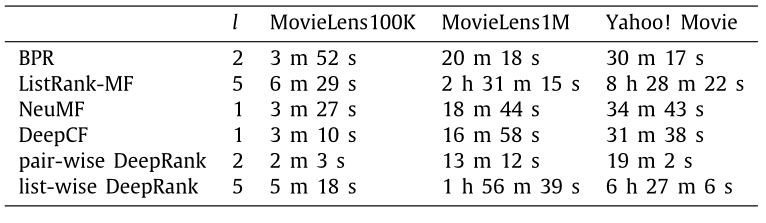
我们发现,深度学习模型确实比矩阵分解模型费时,而相同网络结构下,配对算法又比点预测模型费时,列表排序又比配对模型费时。所以,要根据实际情况选择合适的模型比较好。
最后,我们看一下列表长度对算法的影响:
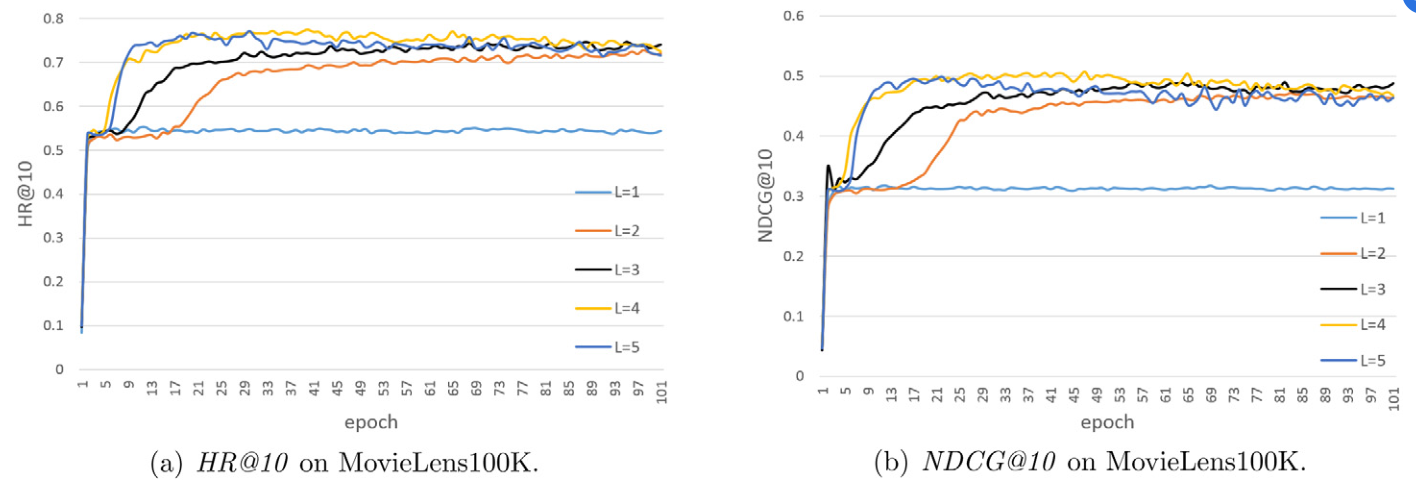
列表长度的情况还是很容易看出来的,长度太短了,不容易得到好结果;太长了容易过拟合。这个数据集中,明显取 3 比较合理。
